Virtual Cell Program
The Braess Paradox
The Braess Paradox is a good illustration of how easily our intuitions about collective interaction can be fooled. It is not a true paradox but rather a counter-intuitive observation about the behaviour of road traffic networks†. The details of this version are cribbed from Bart de Schutter.
Car drivers seek to minimise the time to get from A to B, much as molecules seek to minimise their free energy. Like molecules, car drivers may not be able to act independently of each other: collective interactions may influence individual behaviour. In the network below, there are two symmetrical routes from A to B, each of which consists of a section of road and a bridge.
The road sections are so capacious that the travel time on them is independent of the number of cars and always takes 15 minutes. The bridges, however, are bottlenecks and the time taken to cross each bridge varies in direct proportion to the rate at which cars are crossing it. If X is the flow rate (number of cars per hour) across a bridge, then the time to cross the bridge is X/6000. A steady stream of 1000 cars per hour enters the network at A. How long does it take to get from A to B?
At steady state, each route takes the same amount of time. For, if not, some drivers would switch to a faster route and the system would not be in a steady state. (It is best to imagine that a fixed set of drivers goes through the network repeatedly, as in the morning rush hour, and each driver learns which route is fastest and adjusts his/her behaviour accordingly. The relaxation to the steady state then takes place after all drivers have been through the system many times.) Let L and R be the flow rates on the two routes. Equating the time taken on each route, we find that |
|
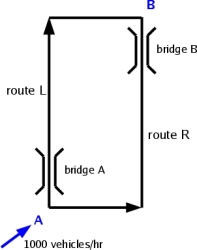 |
15/60 + L/6000 = 15/60 + R/6000
while conservation of cars tells us that
L + R = 1000
It follows that L = R = 500 and the travel time on each route is for everyone.
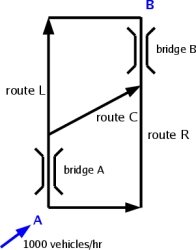
The authorities now decide to build a new super-fast road, shown below, on which the road travel time is only 7.5 minutes.
 |
|
Since drivers have more and better road resources at their disposal they should be able to complete their journeys faster. This logic seems unassailable compared to, say, the basis upon which pharmaceutical companies sometimes choose to develop a new drug.
The travel times at steady state can be calculated as before. There are now three routes, with flow rates L,R and C; the flow rate across bridge A is L+C, while that across bridge B is R+C. Hence,
15/60 + (L+C)/6000 = 15/60 + (R+C)/6000
= 7.5/60 + (L+C)/6000 + (R+C)/6000
L + R + C = 1000 |
from which it follows that L = R = 250 and C = 500. The travel time on each route is now . We see that it is possible to add capacity to a network and make everyone's journey time worse than it was previously!
It is worth noting two points. This example is linear; nonlinearity is neither necessary nor sufficient for counter-intuitive behaviour. Furthermore, the problem arises not with the dynamics but with the behaviour at steady state. The moral of the story is that collective interactions among entities, be they cars or molecules, can yield subtle and unexpected behaviour, for which our intuitions are poorly trained.
It is sometimes pointed out, in the language of game theory, that the Braess Paradox is merely an example of a Nash equilibrium which is not Pareto optimal. That is correct but misses the punch line, which is that the departure from Pareto optimality becomes visible when everyone decides not to use a particular resource (the new road).

